Conférence du mercredi 13 décembre 2006

Programme triple : Prix Sceptiques / Encan / Paradoxes

par F. Benny / M. Toulouse / L. Dubé

Texte annonçant la soirée

Cette soirée, en trois parties, se déroula sous le signe de l'humour :

1. Vote sur les prix Sceptique et Fosse Sceptique 2006

par François Benny

Contrairement aux années précédentes, le deuxième tour de vote pour déterminer les gagnants de ces prix se fera à cette soirée du 13 décembre. Les membres présents pourront voter pour l'un des deux candidats — pour chaque prix — qui auront été choisis au premier tour.

2. Paradoxes logiques

par Louis Dubé

Pendant le compte des votes, on vous présentera des paradoxes confondants liés au scepticisme. Les tenants du paranormal s'en servent parfois pour tenter de nous dérouter. Mieux vaut bien les connaître !

3. Encan d'objets ésotériques

par Michel Toulouse

En deuxième partie de cette soirée, nous tiendrons le populaire encan humoristique du temps des Fêtes. Michel Toulouse, concepteur et fabricant des objets mis en vente, animera la vente aux enchères pour la dixième fois cette année ! Il tente d'illustrer avec un humour toujours subtil, et parfois mordant, certaines thèses paranormales logiquement impensables ou physiquement impossibles. Il le fait en nous proposant des articles surprenants pour faire fuir (ou attirer!) esprits, fantômes, lutins et ovnis.

Si vous avez des objets des encans précédents dont les pouvoirs paranormaux auraient diminué, vous pouvez les rapporter le 13 décembre pour les réactiver et les remettre en vente.

Ce compte-rendu décrira les parties 1 et 3, avant de résumer la deuxième partie.

Annonces

François Filiatrault, l’animateur des soirées sceptiques, en récapitule les objectifs : développer l’esprit critique et cultiver un doute constructif qui permet une connaissance fondée dans la réalité.

Puis, il nous fait part de la récente parution du dernier numéro du Québec sceptique, rempli d’articles aussi instructifs que captivants, en plus de contenir un résumé de conférences récentes. Il ajoute que les membres vont recevoir une convocation à l’assemblée générale annuelle, qui aura lieu le dimanche 18 février à 14 heures au Centre St-Pierre. Il rappelle que ceux qui désirent soumettre une proposition demandant le vote à l’assemblée générale devront le faire avant le 31 décembre 2006. Il mentionne aussi qu’on recherche toujours des idées originales pour les célébrations du 20e anniversaire de la fondation de l’organisme. Tous sont bienvenus à soumettre leurs idées à un membre du conseil.

Actualités

L’animateur propose à notre réflexion quelques chiffres, tirés du Devoir, sur le livre le plus vendu – la Bible – sous la rubrique le « marketing de la parole de Dieu ». La Bible s’est vendue à 47,200 exemplaires français au Canada en 2005-2006, 114,000 en anglais et 23,000 en d’autres langues. Elle a été publiée en 120 langues au Canada, dont 23 autochtones. Aux États-Unis, les ventes se montent à 25 millions de copies en 2005, soit deux fois plus que le dernier Harry Potter, fait remarquer notre animateur. Les Bibles sont astucieusement adaptées à toutes sortes de sous-groupes : surfeurs, couples, cow-boys… Et, depuis Gutenberg, la Bible aurait été traduite en pas moins de 2400 langues ! Nous voilà bien renseignés sur la prétention à l’universalité du message biblique.

Filiatrault poursuit avec la présentation d’un livre au discours opposé au précédent : L’esprit de l’athéisme d’André Comte-Sponville, sous-titre : Introduction à une spiritualité sans Dieu. Il nous en donne un aperçu. Sponville explique pourquoi il est athée, car il croit que Dieu n’existe pas. Quelqu’un qui serait certain que Dieu n’existe pas serait, selon Sponville, un imbécile. Pourtant, il ne se dit pas agnostique. Il aborde les questions suivantes : Peut-on se passer de religion ? Dieu existe-t-il ? Quelle spiritualité pour les athées ? La vraie morale est peut-être celle que nous nous donnons sans avoir besoin de cette béquille céleste, paraphrase notre animateur.

Prix Sceptique et Fosse Sceptique 2006

Par François Benny

François Benny, responsable de cette activité, nous présente brièvement le processus : propositions de candidatures pour chacun de ces prix faites tout au long de l’année par des membres de notre organisme, vote d’acceptation de chaque candidature par le CA, premier tour de vote par les membres en règle ayant une adresse courriel à la fin de novembre, deuxième tour à une soirée sceptique de fin d’année, comme ce soir.

Cette année, 6 propositions pour le prix Fosse Sceptique furent acceptées par le CA et 3 propositions pour le prix Sceptique. En novembre, les membres en règle avec courriel (230) ont voté pour les candidats de leur choix dans les deux catégories de prix. Les deux candidats qui ont eu le plus de votes pour chaque prix sont inscrits sur le bulletin de vote pour le deuxième tour à cette soirée du 13 décembre. Après un court débat sur les mérites des candidats en lice, le vote eut lieu avec les résultats suivants :

Les gagnants pour l’année 2006, sont : prix Sceptique – Luc Chartrand, journaliste à la Société Radio-Canada, pour ses remarquables enquêtes critiques sur certaines pratiques navrantes des médecines douces, présentées aux émissions La Facture et Zone Libre ; et prix Fosse Sceptique – le collège Vanier pour son appui tacite au paranormal en offrant des cours sur les anges, le tarot et la réincarnation.

Détails sur notre site Web à la page des prix :

Encan humoristique d’objets ésotériques

Par Michel Toulouse

Premièrement, Alain Bonnier, co-encanteur extraordinaire, résume brièvement les objectifs de l’encan sceptique : celui-ci représente d’abord une source additionnelle de financement. Il nous permet également de bien nous amuser dans l’esprit du temps des Fêtes, tout en contribuant de façon significative à la santé financière de l’organisme. Tout cela est possible grâce à l’imagination, la persévérance et le talent de l’encanteur principal, Michel Toulouse, concepteur et fabricant des objets mis en vente. Cette année, ce dernier se fait aider par son propre fils, François, pour exhiber les objets ésotériques mis aux enchères et les remettre à l’heureux client contre argent sonnant.

Michel Toulouse, pour la dixième fois cette année, offre des objets surprenants au plus offrant. Il précise, pour ceux qui assisteraient pour la première fois à un tel encan, la raison principale qui sous-tend cet exercice : démontrer l’absurdité des prétentions paranormales en suivant jusqu’au bout la logique aberrante de leurs principes. Voici la liste des nombreux bidules, engins et machins étonnants qui ont tous trouvé preneur à un prix plus que raisonnable :

• Marqueur noir « Anti-Pluton », pour rayer cet astre déchu des livres d’astrologie.
• Para-Lune, pour se protéger de ses effets lunatiques, selon les quartiers.
• Para-Saturne, pour s’abriter des influences enivrantes de ses anneaux.
• Para-Mars, pour se prémunir contre son influence sportive mensongère.
• Crème lunaire, pour prévenir les effets nocifs de longues expositions obscures.
• Tapette à anges, pour les faire fuir lors d’une surabondance débridée.
• Ange gardien de but, pour enpêcher le diable de compter des buts immoraux.
• Ange gardien de sécurité, pour une protection diplômée et compétente.
• Ange gardien de prison, pour surveiller nos fuites incontrôlables dans l’au-delà.
• Capteur de rêves érotiques, pour qu’ils ne s’envolent pas au réveil.
• Capteur de grands rêves, pour nous rappeler notre grandeur imaginaire.
• Capteur de rêves olympiques, pour raviver nos espoirs de médailles.
• Examen de double vue, pour permettre la voyance précise de futurs alternatifs.
• Loto-Psi, « gratteux » pour tester la puissance psi du voyant extra-sensoriel.
• Livre « Da Vinci Code pour les nuls », pour ceux qui n’ont rien compris au polar.
• Livre « Vibrations positives », pour capter les « bonnes » vibrations, Éditions UN ZÉRO.
• Rafraichisseur subliminal, pour détection inconsciente du besoin et action immédiate.
• Encyclopédie Homéo-Folio - tome 1, pour une compréhension lumineuse du feuilleton.
• Piège à fantômes, pour des captures fantasmagoriques de l’évanescente entité.
• Auricu-massage, pour l’oreille paranormalement surmenée en quête de réponses claires.
• Preuves créationnistes : baleine à deux bosses, crabe pianiste, crabe saxophoniste, oiseau totalement gratteur, ours bipolaire – pour démontrer la prévoyance imprévisible du Créateur.
• Téléphone pluricellulaire, pour aller encore plus loin que la simple télépathie neuronale.
• Biscuits chinois faits au Japon, pour découvrir l’ultime vrai secret de la vie…

Paradoxes logiques

Par Louis Dubé

Les paradoxes fascinent, car ils semblent défier nos capacités de raisonnement. Si on suit fidèlement leur logique, on se butera à une contradiction, tel que A = non A, ou à une proposition qui doit être vraie et fausse en même temps.

Ils peuvent aussi parfois servir de point de départ pour une répartie humoristique sur le paranormal. Mais attention, prévient Dubé ! Nous ne sommes pas les seuls à apprécier leurs pouvoirs confondants : les tenants du paranormal peuvent également les utiliser pour tenter de nous dérouter et ainsi ébranler notre scepticisme – si chèrement acquis. Il vaut sans doute mieux pouvoir les distinguer et en comprendre les mécanismes.

Le conférencier nous propose d’en décrire brièvement sept, parmi les plus connus. Il ne prétend pas pouvoir donner une réponse exhaustive aux paradoxes mentionnés. Il offrira seulement une brève explication pour tenter de résoudre l’ambiguïté ou démontrer les limites du raisonnement humain.

Chaque paradoxe sera défini dans un court préambule, suivi d’une question à laquelle l’auditoire pourra répondre par oui ou par non. Une explication sera donnée qu’il sera possible de compléter ou de contester. Dubé s’empresse de mentionner qu’il n’est pas un philosophe professionnel, seulement un amateur intéressé aux leçons qu’on peut tirer des paradoxes.

1. Achille et la tortue

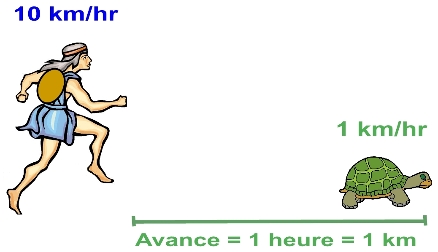
Commençons par un paradoxe classique grec. Probablement un des plus connus : la course logiquement interminable entre Achille et la tortue.

Une tortue (l’histoire n’a pas retenu le nom de cette digne représentante d’une espèce vieille de plus de 200 millions d’années) se déplace à 1 km / hr. Elle a une heure d’avance sur Achille (le célèbre héros grec dont l’histoire a retenu le nom, même si, contrairement à la tortue, il n’a jamais existé). Ce dernier court à 10 km / hr.

Achille pourrait courir plus vite. Mais, il porte un lourd sac à dos contenant son équipement de camping. Il faut quand même rendre les chances égales entre les deux coureurs ! La tortue ne transporte-t-elle pas sa maison sur le dos ? C’est d’ailleurs une championne qui court deux fois plus vite que la plupart de ses congénères.

Achille attend une heure avant de s’élancer à la poursuite de la tortue. Cette dernière aura alors parcouru un kilomètre. Pendant qu’Achille s’époumone à couvrir un premier kilomètre pour tenter de rattraper la tortue, celle-ci aura parcouru un dixième de cette distance, soit 100 mètres. Et pendant qu’Achille se presse à couvrir ces 100 mètres, la tortue se sera éloignée de 10 mètres. Et ainsi de suite… Ce paradoxe a dérouté des générations de philosophes grecs.

Question : Logiquement, Achille pourra-t-il rejoindre la tortue ?

Réponse : Logiquement, non. Intuitivement et mathématiquement, oui.

Si on reste enfermé dans la logique restrictive de l’énoncé du problème, on devra conclure qu’Achille ne pourra pas, en théorie, dépasser la tortue. Pourtant, intuitivement, on sait tous qu’Achille va dépasser la tortue. Et assez rapidement, d’ailleurs.

Mathématiquement, ce paradoxe fait appel à la limite à l’infini d’une somme décroissante, maintenant bien connue en mathématiques. Il s’agit d’une progression géométrique de raison (r) égale un dixième.

La distance de dépassement sera égale à la distance originale divisée par 1 moins la raison de la progression décroissante. Soit : 1000 / (1 – 0.1) = 1111 et 1/9 mètres. On peut également calculer précisément le temps qu’aura pris Achille pour dépasser la tortue, soit : 1111,111 m divisés par 10 000 m/heure fois 60 minutes/heure, soit 6 minutes 40 secondes.

Y a-t-il un lien avec le scepticisme ? Certainement, précise Dubé. L’impasse logique est d’abord résolue par les faits. Achille va dépasser la tortue, c’est un fait indéniable. Les faits constituent l’ultime référence de vérité, par delà la logique confondante.

Un membre de l’assistance fait remarquer que si les Grecs n’ont pu résoudre ce problème, c’est qu’ils n’avaient pas développé les outils mathématiques pour le faire. Une personne qui n’aurait pas aujourd’hui des connaissances mathématiques suffisantes pour résoudre ce problème pourrait également être confondue, fait remarquer le conférencier.

2. Le barbier raseur

Passons maintenant à un deuxième paradoxe, encore plus confondant que le premier, précise Dubé. L’énoncé se lit comme suit :

Le barbier du village rase tous les hommes du village qui ne se rasent pas eux-mêmes, et personne d’autre. Se rase-t-il lui-même ?

Le paradoxe se définit par cette argumentation confondante : si le barbier du village se rase, il rase un homme du village qui se rase lui-même. S’il ne se rase pas, il ne rase pas tous les hommes du village qui ne se rasent pas eux-mêmes.

Ce genre de paradoxe est dit « autoréférentiel ». Il n’a pas été résolu. Bertrand Russell proposera la théorie des types pour tenter de résoudre ce paradoxe, mais les diverses solutions qu’il a avancées demeurent controversées. On doit tout simplement conclure qu’un ensemble ne peut être membre de lui-même. Tentons de reconnaître ce paradoxe pour ce qu’il est pour ne pas s’y empêtrer.

Voici d’ailleurs d’autres formes du même genre de paradoxe, il s’agit également de phrases autoréférentielles :

• Épimenide, le Crétois, déclare : « Tous les Crétois sont des menteurs ».
• Le catalogue de tous les catalogues non catalogués se contient-il lui-même ?
• Les humains apprennent de l’histoire qu’ils n’apprennent rien de l’histoire.
• Ou encore plus simple : cette affirmation est fausse.

3. La poule ou l’œuf

Ceux qui ont assisté au débat entre créationnistes et évolutionnistes, en mars 2006, se souviendront du paradoxe avancé, sourire en coin, par le créationniste en chef du Québec, Laurence Tisdall : « Qu’est-ce qui vient avant, la poule ou l’œuf ? »

Paradoxe classique s’il en est un ! Il faut une poule pour pondre un œuf – le poussin, qui deviendra poule, provient de l’œuf.

Réponse créationniste : il y eut une première poule… et un premier coq, créés par Dieu. Ce couple d’heureux futurs parents se maria. De cette union bénie naquirent de nombreux beaux et jeunes poussins. Cela constitue le début de la lignée des poules jusqu’à aujourd’hui, sur une période d’environ 10 000 ans.

Réponse évolutionniste : l’œuf vient en premier. Car une mutation aléatoire peut produire un œuf de poule de parents qui n’étaient pas tout à fait « poule et coq », mais presque. Les poules sont d’ailleurs des oiseaux issus des dinosaures qui pondaient aussi des œufs. Cette évolution s’est faite très progressivement au cours de millions d’années.

Pour paraphraser le biologiste Cyrille Barrette : « Il n’y a pas plus de première poule que de premier francophone ! » Le concept même de première poule suppose déjà une création et évacue l’idée d’évolution. Il y a aujourd’hui des millions de francophones, mais il n’y a jamais eu de premier francophone. Le français a évolué du latin sous influence germanique pendant des centaines d’années.

4. Le voyant déterministe

Voici un paradoxe qui nous fait réfléchir sur les conséquences d’une vraie voyance : « Si un voyant voit votre avenir, c’est que votre avenir existe déjà. » Cela est encore plus vrai d’un Dieu omniscient. Sommes-nous alors vraiment libres de nos actions ?

Paradoxe : dans le cas du voyant ou de Dieu, si le pouvoir de voir l’avenir était réel, nos actions futures seraient déterminées.

Réponse : oui, nous sommes libres ! Et le conférencier de soulever une chaise vide, puis de la laisser tomber dans un grand fracas. Qui avait prévu qu’il aurait posé de geste ? Personne, mais encore : après l’avoir soulevé, ne fallait-il pas tôt ou tard la déposer ? Prenant l’objection au mot, le conférencier souleva une seconde fois la chaise, et, cette fois-ci, la déposa tranquillement pour la faire reposer sur deux pattes à angle aigu sur une autre chaise. Geste encore une fois imprévisible, clame-t-il !

Évidemment, pour éviter le paradoxe, un voyant ne pourrait prétendre qu’à une forte probabilité de réussite, à une simple tendance dont il ne voudra pas préciser la probabilité de succès. Pourtant, même si sa vision de l’avenir est floue, il voit un avenir déjà fixé. D’autre part, si le voyant soutient qu’il voit exactement l’avenir, mais qu’on peut le changer, son affirmation devient irréfutable et ses prévisions inutiles, répond le conférencier à un commentaire de l’auditoire.

Il existe aussi une vision matérialiste du paradoxe : tout événement a une cause. Donc, tout était en place dès le Big Bang et les résultats auraient été déterminés jusqu’à maintenant par les seules lois causales. Que répondre à ce point de vue réductionniste fort controversé, débattu sans succès maintes fois par de multiples philosophes à travers les âges ?

On peut proposer une réponse simple, suggère le conférencier : le futur est imprévisible pour nous, car la complexité des interactions matérielles en rend l’analyse trop complexe. N’oublions pas, suggère-t-il, que les plus puissants ordinateurs ne peuvent prédire la météo plus de 5 jours à l’avance, en se trompant la moitié du temps. On y reconnaît bien un système chaotique parfaitement déterminé, ajoute un auditeur, mais on n’a pas la capacité de calcul pour prédire ses états futurs.

Un autre membre de l’auditoire proposera que tous les scénarios possibles existent dans une infinité d’univers parallèles inaccessibles. Le principe de parcimonie d’Occam suggère un seul univers déchiffrable, rétorque Dubé. Les faits semblent indiquer que nous sommes en général libres d’agir comme il nous plaît, conclut-il, et, pour un sceptique, les faits sont l’ultime référence.

5. Le paradoxe du paranormal

Certains prétendants au Défi Sceptique soutiennent que l’exigence de démontrer clairement un don paranormal est malhonnête. Car, les sceptiques insistent que l’expérience soit reproductible. Si un phénomène paranormal est un jour démontré de cette façon, il deviendra un phénomène physique normal – auparavant inconnu, maintenant connu.

Le paranormal peut-il exister ? Un événement paranormal reproductible devient effectivement normal. Par contre, un vrai événement paranormal ne peut s’observer que très rarement. L’élément paradoxal réside dans l’exigence de reproductibilité d’un phénomène qui ne peut l’être.

Le conférencier affirme que le paranormal peut exister, à l’intérieur d’un processus de démonstration, si on observe qu’il défie des principes physiques connus, tels que la gravité, la conservation de l’énergie ou la thermodynamique. Pourtant, on n’a pas encore trouvé de phénomènes paranormaux reproductibles sous des conditions contrôlées. On n’est donc pas malhonnête d’offrir, ici au Québec, 10 000 $ à quiconque pourra démontrer que son don paranormal va à l’encontre des lois connues de la nature.

6. Preuves d’inexistence

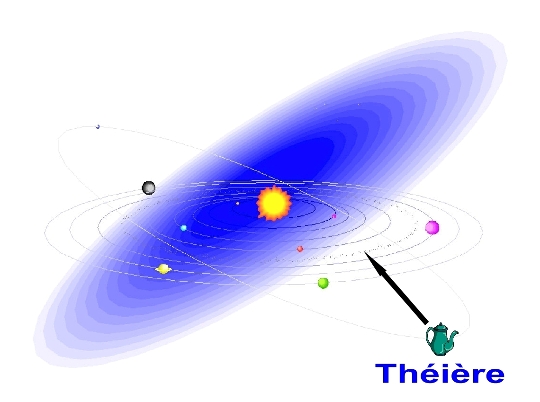
On demande souvent aux Sceptiques de croire à des phénomènes qui n’existent pas. Notre première réaction est de laisser au prétendant le fardeau de la preuve. Et d’ajouter, à l’instar de Sagan : « Que des prétentions extraordinaires exigent des preuves extraordinaires ! » Mais la question philosophique demeure : peut-on prouver que quelque chose n’existe pas ?

Le paradoxe se trouve dans le fait suivant : si une chose n’existe pas, elle ne laissera forcément aucune trace. Par contre, l’absence de traces ne prouve pas l’inexistence, puisqu’aucune recherche de traces ne pourra prétendre être absolument exhaustive. Bertrand Russell, le philosophe agnostique anglais, en a donné un exemple mémorable : il postula l’existence d’une théière en orbite autour du Soleil entre Mars et Jupiter, dans la ceinture d’astéroïdes. Prouvez-moi le contraire, se serait-il exclamé !

La réponse théorique est, bien sûr, non : on ne peut prouver l’inexistence de quoi que ce soit. On ne peut évidemment examiner tous les lieux où une chose pourrait se trouver pour ainsi en conclure qu’elle n’existe pas. L’entité pourrait d’ailleurs se trouver au-delà de nos capacités sensorielles physiques et temporelles.

Toutefois, ce n’est pas parce qu’on ne peut prouver qu’une chose n’existe pas, qu’on doive conclure qu’elle existe vraiment. Le sceptique doit-il alors se résigner à demeurer désespérément agnostique (a-thé-ière, fait remarquer un auditeur) de la théière de Russell, tout comme de Dieu ?

Le conférencier suggère que, de façon pratique, on peut raisonnablement conclure à l’inexistence d’une entité postulée si on observe des traces contradictoires à son existence. Il donne deux exemples liés au créationnisme : 1. l’inexistence d’une « jeune Terre », 2. l’inexistence d’un créateur juste et bon. Dans le premier cas, la lente dérive observée des continents ne peut s’être produite en si peu que 10 000 ans. Dans le deuxième cas, la cruauté prédatrice observée du monde animal ne peut avoir été planifiée par un Dieu juste et bon. Les traces observées sont contradictoires aux thèses avancées.

7. Le pont

Terminons sur une note légère, comme nous avons commencé. Voici un dernier paradoxe classique faisant référence à la philosophie grecque, celui du « pont ». Il met en scène deux grands philosophes : Socrate et Platon.

Socrate veut traverser un pont. Platon, son disciple, bien planté sur le pont, lui barre la route. Ce dernier défie son maître par ces paroles : « Si les prochains mots que tu dis sont vrais, je te laisse traverser. Sinon, je te jette à l’eau. » Socrate lui répond du tac au tac : « Tu vas me jeter à l’eau. »

Platon peut-il jeter Socrate à l’eau sans se contredire ? Dérouté, le laissera-t-il passer ? De quel type de paradoxe s’agit-il ? Le conférencier laisse l’auditoire méditer sur les limites de la raison humaine…

Conclusions

Certains paradoxes peuvent être résolus, d’autres pas. Les mathématiques modernes peuvent souvent expliquer certaines paradoxales régressions à l’infini. Mais, la logique se bute parfois à des énoncés autoréférentiels qui la confondent.

Tout appel au concept d’infini risque de conduire à un cul-de-sac logique. Par exemple, les concepts de toute-puissance et d’omniscience génèrent toutes sortes de paradoxes logiques.

Heureusement, la réalité demeure cohérente. On ne sait pas pourquoi les lois physiques sont ce qu’elles sont, mais elles ne changent pas. Ultimement, les paradoxes trouvent leur réponse dans la réalité des faits. S’il n’y a pas de faits, on doit demeurer sceptique.

Référence : Paradoxes from A to Z, Michael Clark, 2002, Routledge, London.

Compte-rendu rédigé par Louis Dubé